一、前言:什么构成了“学习”?
机器学习的核心任务是:从数据中自动学习一个映射函数,使其能对新样本做出准确预测。
实现这一目标并非魔法,而是由三大基本构件系统性协作完成:
- 模型假设(Hypothesis Space):定义我们可以选择的函数族
- 评价函数(Loss Function / Objective Function):衡量模型预测与真实值的差距
- 优化算法(Optimization Algorithm):调整模型参数以最小化评价函数
这三者构成了机器学习的“理论支架”,贯穿算法设计、模型训练、性能优化等所有关键环节。
二、模型假设:选择什么函数来学习?
定义
模型假设(Hypothesis)定义了我们用来拟合数据的函数族,也称为假设空间 H\mathcal{H}H。每个候选函数都是一种对现实数据生成机制的近似建模。
举例

作用与影响
- 决定模型的表达能力和拟合上限
- 假设空间太小 → 欠拟合;太大 → 容易过拟合
三、评价函数:如何衡量模型的优劣?
定义
评价函数(又称目标函数、损失函数)用于衡量模型预测值与真实标签之间的误差,是训练过程中待最小化的目标。
常用损失函数示例

评价函数的设计原则
- 与任务目标一致(如分类用概率分布的交叉熵)
- 可导,便于梯度计算
- 对异常值鲁棒(如使用Huber Loss)
四、优化算法:如何实现学习过程?
定义
优化算法负责在模型假设空间中,寻找使损失函数最小的模型参数。常用的是基于**梯度下降(Gradient Descent)**的算法。
优化方法对比
| 优化算法 | 特点 |
|---|---|
| SGD(随机梯度下降) | 每次只用一个样本,速度快但不稳定 |
| Mini-batch SGD | 平衡计算效率与梯度波动,是主流方案 |
| Adam | 自适应学习率,收敛更快,适合大规模神经网络 |
| L-BFGS、Momentum | 增加记忆项,加速收敛但适用范围有限 |
优化算法的影响
- 决定收敛速度与稳定性
- 影响是否能跳出局部最优、避免梯度消失/爆炸问题
- 与模型结构和损失函数高度耦合
五、三者协同构成完整学习流程
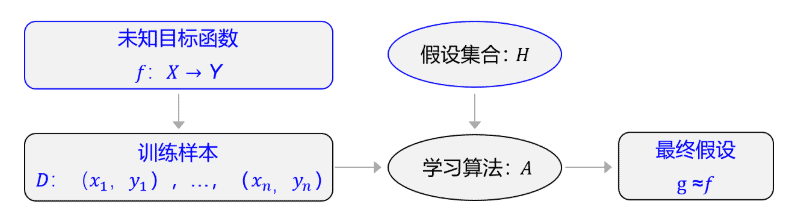
机器执行学习任务的框架体现了其学习的本质是“参数估计”(Learning is parameter estimation),从假设集合H中,通过学习算法A找到一个函数g。如果g能够最大程度的拟合训练样本D,那么可以认为函数g就接近于目标函数f。

六、实践示例:Keras 构建图像分类模型
以下是三要素在实际工程中的体现(以 TensorFlow/Keras 为例):
# 模型假设:定义模型结构(一个简单CNN)
model = keras.Sequential([
keras.layers.Reshape((28, 28, 1), input_shape=(28, 28)),
keras.layers.Conv2D(32, (3, 3), activation='relu'),
keras.layers.Flatten(),
keras.layers.Dense(10, activation='softmax')
])
# 评价函数:交叉熵 + 优化算法:Adam
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
# 启动训练(优化参数)
model.fit(x_train, y_train, epochs=5)
七、总结与延伸
| 要素 | 功能 | 常见设计选择 |
|---|---|---|
| 模型假设 | 决定学习函数的类型与复杂度 | 线性模型、树模型、神经网络等 |
| 评价函数 | 衡量模型预测质量,指导优化方向 | MSE、交叉熵、Hinge Loss 等 |
| 优化算法 | 寻找最优参数,推动模型逼近目标 | SGD、Adam、RMSprop 等 |
这三者不仅支撑了所有机器学习算法的底层逻辑,也是我们理解新模型(如Transformers、Diffusion Models等)时的起点。